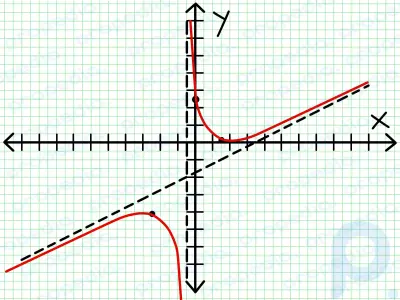
有理関数は、y = N(x)/D(x) の形式をとる方程式です。ここで、N と D は多項式です。正確なグラフを手でスケッチしようとすると、基本的な代数学から微分積分まで、高校数学の最も重要なトピックの多くを包括的に復習することになります。次の例を考えてみましょう: y = (2x - 6x + 5)/(4x + 2)。
ステップ
-
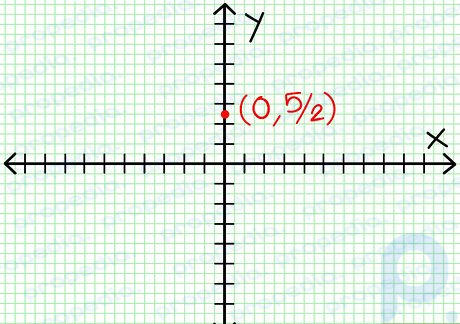
Google 画像 ステップ 1 y 切片を見つけます。 -
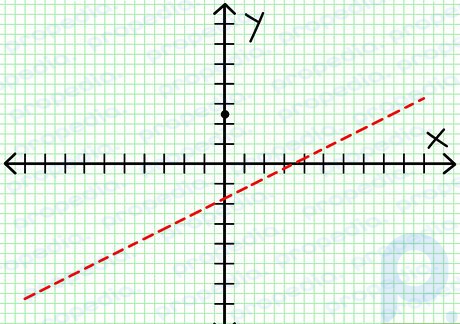
Google 画像 ステップ 2 水平方向の漸近線を見つけます。 - 分子の次数が分母の次数より小さい場合、除算は行われず、漸近線は y = 0 になります。
- deg(N) = deg(D) の場合、漸近線は主要な係数の比率で水平線になります。
- deg(N) = deg(D) + 1 の場合、漸近線は、傾きが主要係数の比である直線になります。
- deg(N) > deg(D) + 1 の場合、|x| の値が大きい場合、y は二次、三次、またはより高次の多項式としてすぐに正または負の無限大になります。この場合、除算の商を正確にグラフ化することはおそらく価値がありません。
-
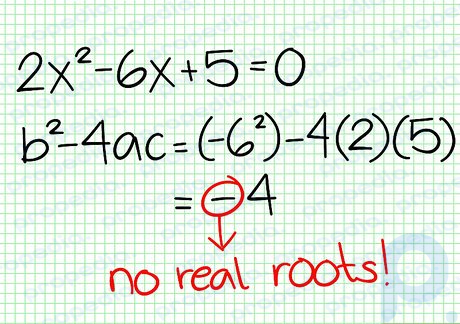
Google 画像 ステップ 3 ゼロを見つけます... -
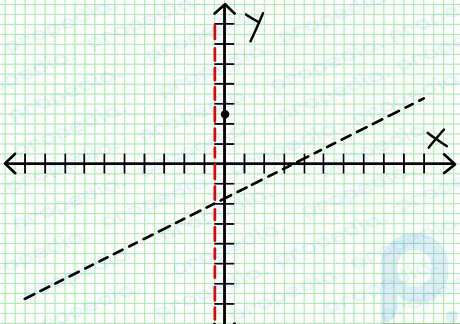
Google 画像 ステップ 4 垂直方向の画像を見つけます... -
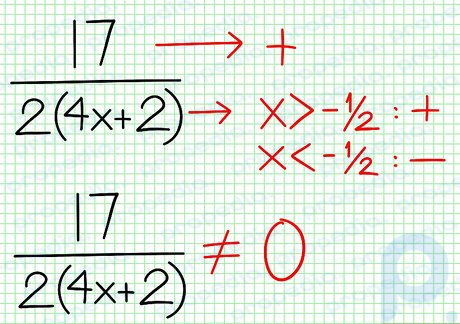
Google 画像 ステップ 5 ステップ 2 の割り算の残りを見てください。 -
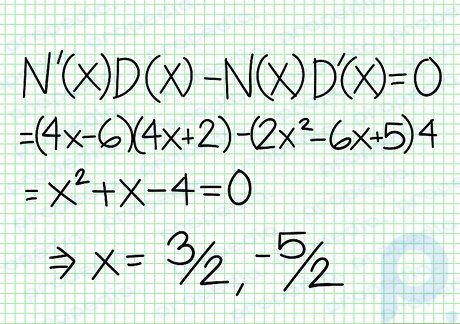
Google 画像 ステップ 6 局所極値を見つけます。 -
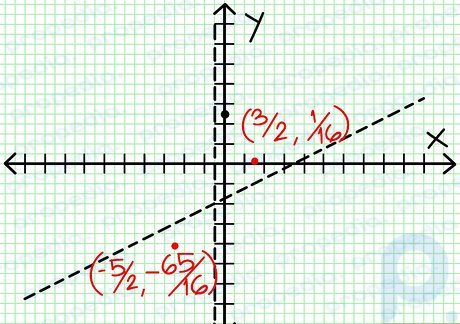
Google 画像 ステップ 7 各極値の y 値を見つけます。 -
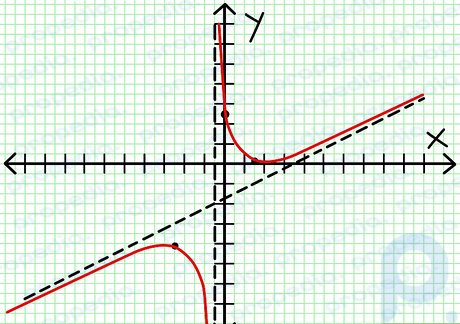
Google 画像 ステップ 8 点を結ぶ